The Ethereum co-founder, Vitalik Buterin, expects further enhancements in the proving techniques based on binary fields in the months ahead. The co-founder discussed a new cryptographic proving system which will be more efficient for zero-knowledge proofs.
A post shared by Buterin on April 29 in which he introduced “Binius” for making cryptographic proofs more efficient than binary fields. The introduction of Binius will boost the performance over old-proof systems such as zk-SNARKs.
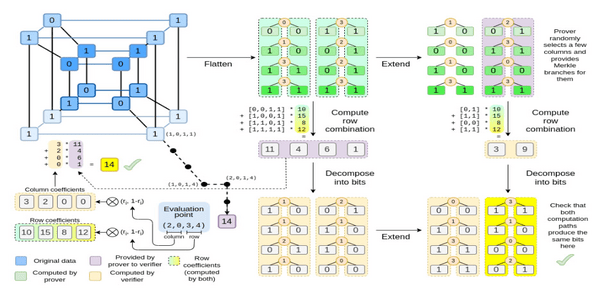
The key factor of Binius is that it is capable of performing actions over binary bits, instead of over larger numbers. This proof system is different from traditional systems like SNARKs and STARKs, which work on larger numbers like 64-bit or 256-bit integers.
Buterin explains the underlying data that the process consists of small values like counters, indices, and boolean flags. By using Binius, it will process bits directly, resulting in higher efficiency.
Source: Vitalik Buterin
Buterin explains that the new proofing system brings enhancements by representing data as a multidimensional “hypercube” composed of bits. It also uses binary “finite fields” to enable quick mathematical operations on bits and sequences of bits.
It uses a special way of turning bit-level data into a form that works well for “polynomial” processing and Merkle proofs. This process keeps the efficiency advantages of working with binary data.
The binary system improves the core arithmetic of cryptographic proof systems by performing complex cryptographic applications efficiently.
The Polynomial mechanism is used in zk-proofs for encoding data and computations. This mechanism enables the verification of proofs without exposing the original information, hence the term “zero knowledge.”
Benjamin E. Diamond and Jim Posen initially proposed the concept in a 2023 whitepaper titled “Succinct Arguments over Towers of Binary Fields.”
The use of Binius is to interpret data more efficiently than traditional systems and to do binary-level computations
“I expect many more improvements in binary-field-based proving techniques in the months ahead,” Buterin concluded.

